
Fixed Point Iteration (Iterative) Method Algorithm.Secant Method Python Program with Output.Newton Raphson Method Online Calculator.Regula Falsi or False Position Method Online Calculator.Python Program for Regula False (False Position) Method.MATLAB Program for Regula False (False Position) Method.C++ Program for Regula False (False Position) Method.C Program for Regula False (False Position) Method.

Pseudocode for Regula Falsi (False Position) Method.

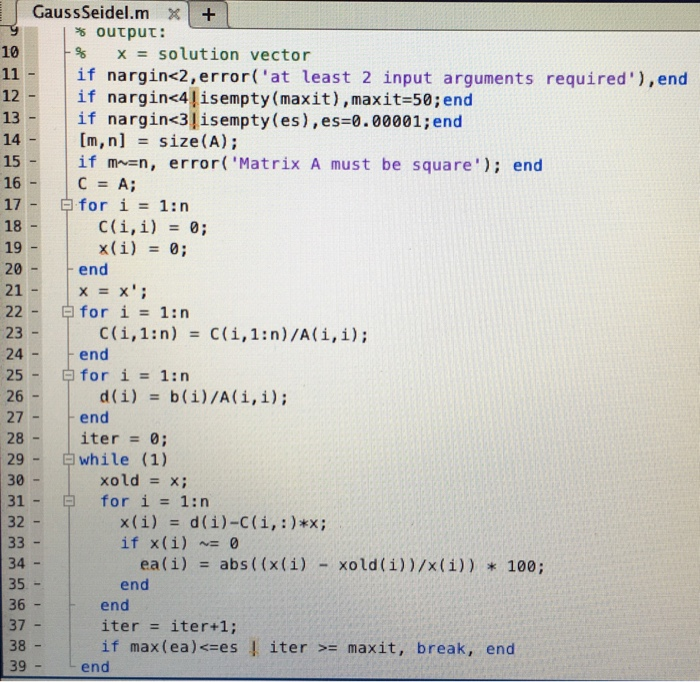
Algorithm for Regula Falsi (False Position Method). The following code utilizes the procedure “GS” that takes a matrix, a vector, and a vector of some guesses to return the new guess for the components of the vector. Using forward substitution in the equation, then, the component in iteration can be computed as follows: It is not obvious in this example, but the Gauss-Seidel method can converge faster than the Jacobi method. Therefore, the system converges after iteration 4 similar to the Jacobi method. The relative approximate error in this case is Notice that in forward substitution, the value of uses the value for and that uses the values of and : Then, the initial guesses for the components are used to calculate the new estimates using forward substitution. First the system is rearranged to the form: The Gauss-Seidel method with a stopping criterion of will be used. The same stopping criterion as in the Jacobi method can be used for the Gauss-Seidel method. If we start with nonzero diagonal components for, then can be used to solve the system using forward substitution: The left hand side can be decomposed as follows:Įffectively, we have separated into two additive matrices: where is an upper triangular matrix with zero diagonal components, while is a lower triangular matrix with its diagonal components equal to those of the diagonal components of. First notice that a linear system of size can be written as: This is different from the Jacobi method where all the components in an iteration are calculated based on the previous iteration. In the Gauss-Seidel method, the system is solved using forward substitution so that each component uses the most recent value obtained for the previous component. The Gauss-Seidel method offers a slight modification to the Jacobi method which can cause it to converge faster. Open Educational Resources Iterative Methods: Derivatives Using Interpolation Functions. High-Accuracy Numerical Differentiation Formulas. Basic Numerical Differentiation Formulas. Linearization of Nonlinear Relationships. Convergence of Jacobi and Gauss-Seidel Methods. Cholesky Factorization for Positive Definite Symmetric Matrices.







 0 kommentar(er)
0 kommentar(er)
